Ibland när man arbetar med analyser får man fram en del resultat som inte passar in i det man skriver. Jag har tänkt lägga ut en del olika resultat av det slaget här i bloggen den närmaste tiden. Några sådana överblivna resultat kommer från en artikel om Sverigedemokraterna som jag har skrivit tillsammans med statsvetarna Gissur Erlingsson och Kåre Vernby och som jag får återkomma till i något senare inlägg.
Som en del i den artikeln har vi studerat partiernas röstsammanhållning i riksdagen, dvs. i vilken grad riksdagsledamöterna röstar på samma sätt inom respektive parti. Detta är ett forskningsområde som har fått större uppmärksamhet inom den amerikanska statsvetenskapen (se t.ex. studier av roll call data och ideal point estimation) än i den svenska, vilket inte är så konstigt då partierna har en mer central roll i den svenska politiken. Det finns dock svenska studier som är intressanta (exempelvis av professor Sören Holmberg) och kanske kommer det vid Linnéuniversitetet pågående forskningsprojektet kring riksdagens partigrupper att nå nya, intressanta resultat.
I vilket fall, det vanligaste sättet att mäta sammanhållning i röster är med hjälp av det så kallades Rices index. Namnet har inget med ris att göra, utan det är uppkallat efter upphovsmannen Stuart A Rice. I hans bok Quantitative methods in politics från 1928 beskriver han detta index. Det är väldigt enkelt: man tar den absoluta skillnaden mellan antalet ja- respektive nej-röster och delar den skillnaden med summan av ja- och nej-röster. Om sammanhållningen är minimal innebär det att det är lika stort antal ja- och nej-röster, och det blir då noll i täljaren och indexet blir också noll. Om det endast finns ja-röster eller endast nej-röster, dvs. sammanhållningen är totalt, då blir det samma tal i täljare och nämnare och indexet blir följaktligen 1. Det kan även uttryckas mer elegant i en formel, där Y står för ja-röster och N för nej-röster.
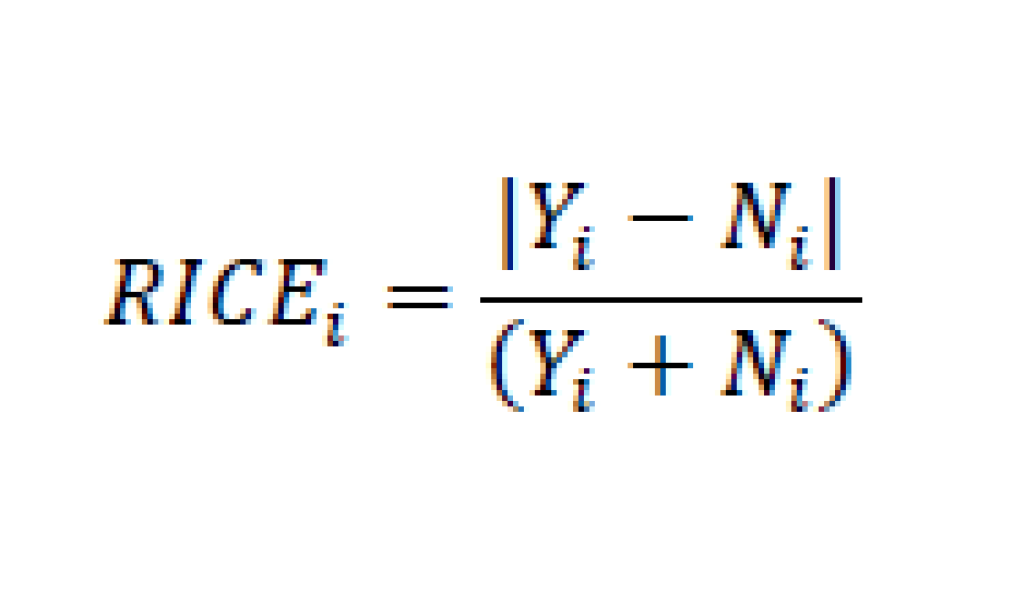En nackdel med Rices index när man ska studera Sveriges riksdag är att det är baserat på två utfall: ja eller nej. I riksdagen finns även möjligheten att avstå, vilket gör att de möjliga utfallen blir tre. Born och Nevison (1973) föreslår (utifrån Brams & O’Leary, 1970) något som kan beskrivas som ett kvadrerat Rices index och som kan hantera flera olika utfall. Personligen tycker jag att det indexet har en del egenskaper som inte är tilltalande. Men det finns även andra mått att överväga. I vår studie har jag valt att använda “Agreement index” som lanserats av Hix, Noury och Roland (2005) vid studier av röstning Europaparlamentet. Det kan uttryckas enligt nedanstående formel, där Y står för ja-röster, N för nej-röster och A för dem som avstår att rösta. Man får då bortse dem som inte är närvarande. Då kvittningssystemet ibland används i riksdagen för att ledamöter inte ska tvingas rösta mot sin övertygelse kan man invända att sammanhållningen överskattas. Å andra sidan är det om inte omöjligt så i alla fall mycket svårt att veta i vilka fall kvittning används på det sättet.
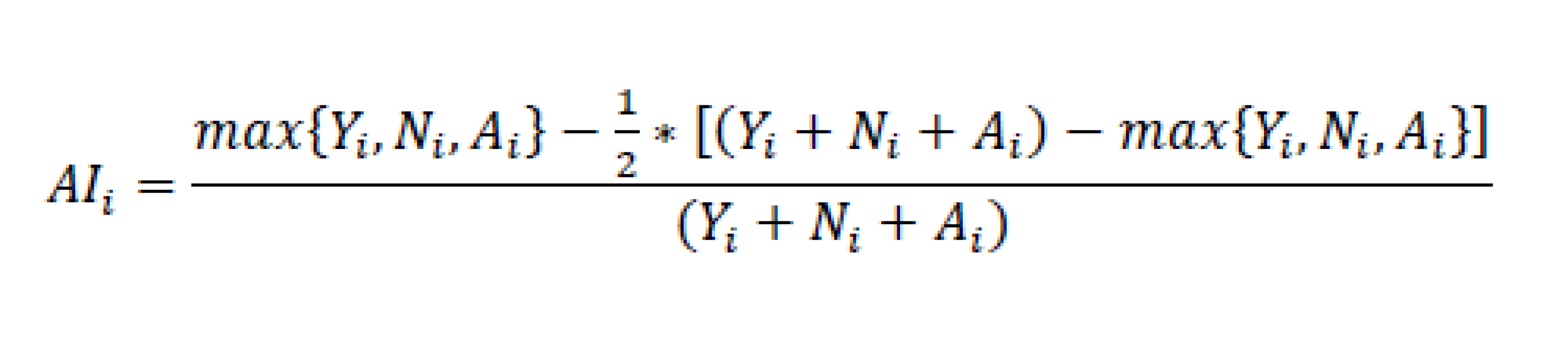
Om man tänker sig 90 röstande och alla röstar ja, så blir indexet (90-0,5(90-90))/90=1. Om rösterna fördelar sig 30, 30 och 30, så blir indexet ((30-0,5(90-30))/90=0. Med andra ord varierar indexet 0 och 1, där 0 innebär maximal röstsplittring och 1 innebär maximal röstsammanhållning. Om man vill att indexet ska gå från 0 till 100 är det bara att multiplicera med 100. Man kan sedan räkna fram detta index för ett parti vid ett antal omröstningar och sedan ta fram medelvärdet av dessa index. Detta är precis vad vi gjort för samtliga riksdagspartier, men jag sparar resultaten till nästa blogginlägg.