Häromveckan fick jag frågan om hur man på bästa sätt gör ett venndiagram där cirklarna är proportionella i förhållande till gruppernas storlek (om du inte känner till venn- och eulerdiagram, se ett av mina tidigare inlägg). Jag är inte helt säker på om jag tycker att det är en strålande idé över huvud taget. Om man vill illustrera olika gruppers storlek är cirklar inget bra alternativ (en dag kanske den insikten även kommer till DN:s grafiker, även om jag börjar ge upp hoppet). Men om det inte är huvudsaken kan det kanske ändå ge en ungefärlig uppfattning av den inbördes storleksordningen.
Om man googlar efter “venn diagram area proportional” hittar man ett gäng lösningar, både sådana där man skapar diagrammet på webben i en applikation och sådana där man laddar ned ett särskilt program. Det innebär dock manuellt arbete som är svårt att reproducera eller inlärning av ett nytt program och de kostnader som är förenade med det. Nyligen gav jag lite vägledning när det gäller hur man ska välja statistikprogram. Såvitt jag vet är det bara ett av dessa program där man kan skapa proportionella venndiagram (eller eulerdiagram), och det är R. Där finns dock åtminstone två olika paket att använda sig av: venneuler och vennDiagram. I det första är koden väldigt enkel. Säg att vi vill skapa ett venndiagram med A, B och C, där storleken för de tre är 200, 400 respektive 800. Och där kombinationen A, B och C är 20, kombinationen A och B är 40, A och C är 80 och B och C är 80. Då blir koden i R följande:
require(venneuler) v <- venneuler(c(A=200, B=400, C=800, “A&B&C”=20, “A&B”=40, “A&C”=80, “B&C”=80)) plot(v)
Resultatet blir som följer:
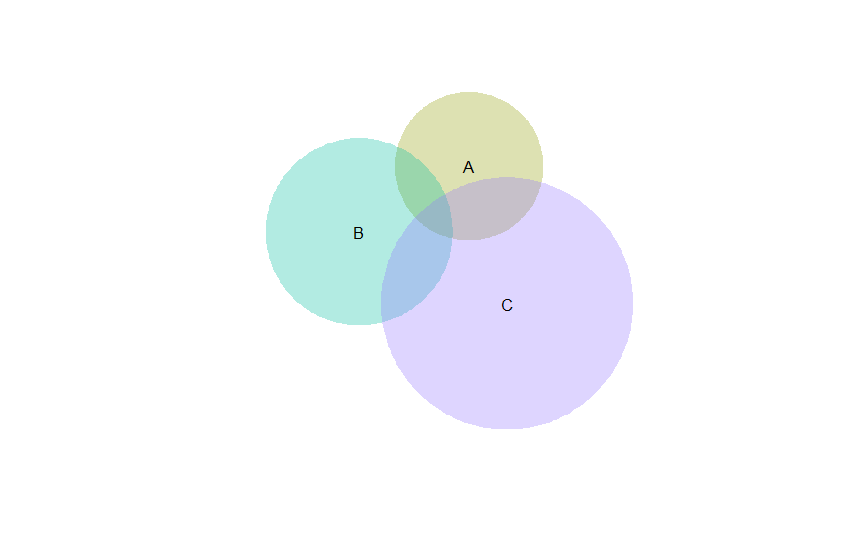
Ibland sätter geometrin gränser som gör att den figur som skapas inte exakt stämmer överens med vad som specificeras, så det gäller att kolla att det verkar stämma. Det går att fixa till mer kring färger och utseende, antingen i R-koden eller senare i något annat program som Inkscape (som liksom R är gratis (den som har bättre resurser kan använda Adobe Illustrator)). Möjligheterna att kontrollera utseendet är än större om man använder paketet vennDiagram istället. Men som ni ser, R är inte alltid så krångligt och det finns oftast fler lösningar på olika problem, även om antalet lösningar ibland kan vara överväldigande.