Med det ökande intresset för visualiseringar av data har Euler- och framför allt Venndiagrammen fått en renässans. Det har på senare tid skrivits en del bra om dessa diagram på olika håll, så jag passar på att skriva ned några rader och ge ett par länkar (se längst ned).
Venndiagram är diagram som visar alla logiskt möjliga kombinationer mellan mängder (klasser). De används flitigt i mängdlära. Vanligen tar de formen av två eller tre överlappande cirklar. I bilden nedan ses ett Venndiagram med cirkel A och B.
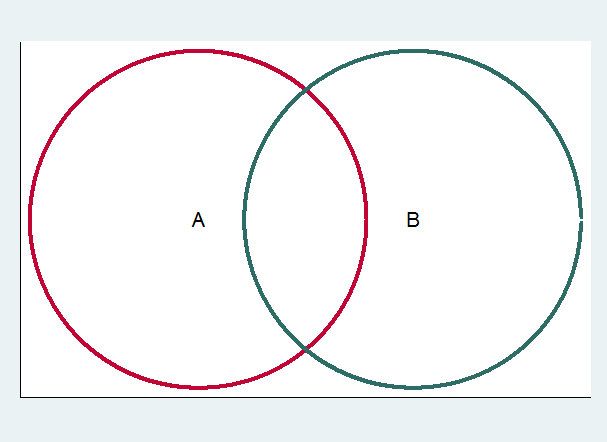
Allt som befinner sig inom cirkel A tillhör en viss kategori (eller mängd) och allt som befinner sig utanför cirkeln tillhör inte den kategorin. Samma gäller för cirkel B. Exempelvis kan vi tänka oss att cirkel A representerar hundar och cirkel B skådespelare. Den del av diagrammet faller inom både cirkel A och B brukar kallas snittet av A och B och avser dem som tillhör både kategori A och B, vilket i det här exemplet blir skådespelande hundar, såsom Rin Tin Tin, Lassie och Uggie. Den del av diagrammet som är inom antingen A eller B (tillhör minst en av kategorierna) brukar kallas unionen av A och B. Eftersom Venndiagram ska innehålla alla logiskt möjliga kombinationer av de kategorier som redovisas blir det komplext om antalet kategorier är många, så vanligen innehåller diagrammen två eller tre kategorier (ofta i form av cirklar).

Bilden ovan är hämtad från The World Reduced to Infographics av Patrick Casey och Worm Miller.
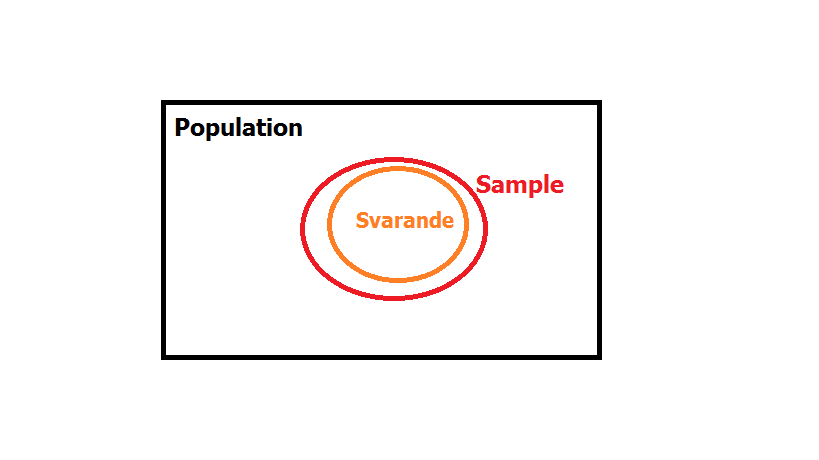
Venndiagram kan ses som en underkategori till Eulerdiagram. Eulerdiagram behöver inte ha restriktionen att diagrammet ska innefatta alla möjliga kombinationer av de olika klasser som redovisas. De innefattar därmed fler typer av diagram än Venndiagram. Eulerdiagram brukar bland annat användas för att beskriva statistiska urvalsundersökningar, som i bilden nedan. Där har vi hela populationen, t.ex. svenska medborgare 18 år och äldre, ur vilken vi drar ett urval (sample). De som ingår i urvalet kontaktas sedan på något sätt, men tyvärr vill inte alla vara med i undersökningen, så de svarande blir en delmängd av dem i urvalet. Ofta komplicerar man bilden ytterligare genom att skilja på den population vi avser att undersöka och den population som ingår i den urvalram (den lista från vilken vi drar urvalet) vi har att tillgå när vi gör undersökningen.
Det är förhållandevis enkelt att skapa ett Venn- eller Eulerdiagram i en mängd programvaror. Vanligen är inte kategorierna redovisade i storlekar som är proportionella mot deras faktiska storlekar. Om man ändå vill ha mer kontroll över proportionerna och även vill koppla dem till befintliga data är alternativen färre. I statistikprogrammet Stata finns det användarskrivna kommandot -pvenn-, som kan installeras via -ssc install pvenn- och som kan ta fram Venndiagram. Tyvärr blir det inte riktigt så snyggt som man skulle önska (diagrammet med cirkel A och B ovan är skapat i Stata). I statistikprogrammet R (fantastiskt gratisprogram) finns däremot funktionen venneuler() som kan hantera både Venn- och Eulerdiagram och dessutom resulterar i ett riktigt snyggt resultat.
Venndiagram kan ofta användas för att illustrera roliga samband, som i diagrammet av Stehpen Wildish nedan (se fler Venndiagram av Stephen Wildish här).

_Läs bra inlägg om Euler- och Venndiagram hos visual.ly och EagerEyes. Även Wikipedia har matnyttig information om Venndiagram och Eulerdiagram. För den som blir riktigt biten rekommenderas den tredje internationella workshopen kring Eulerdiagram._